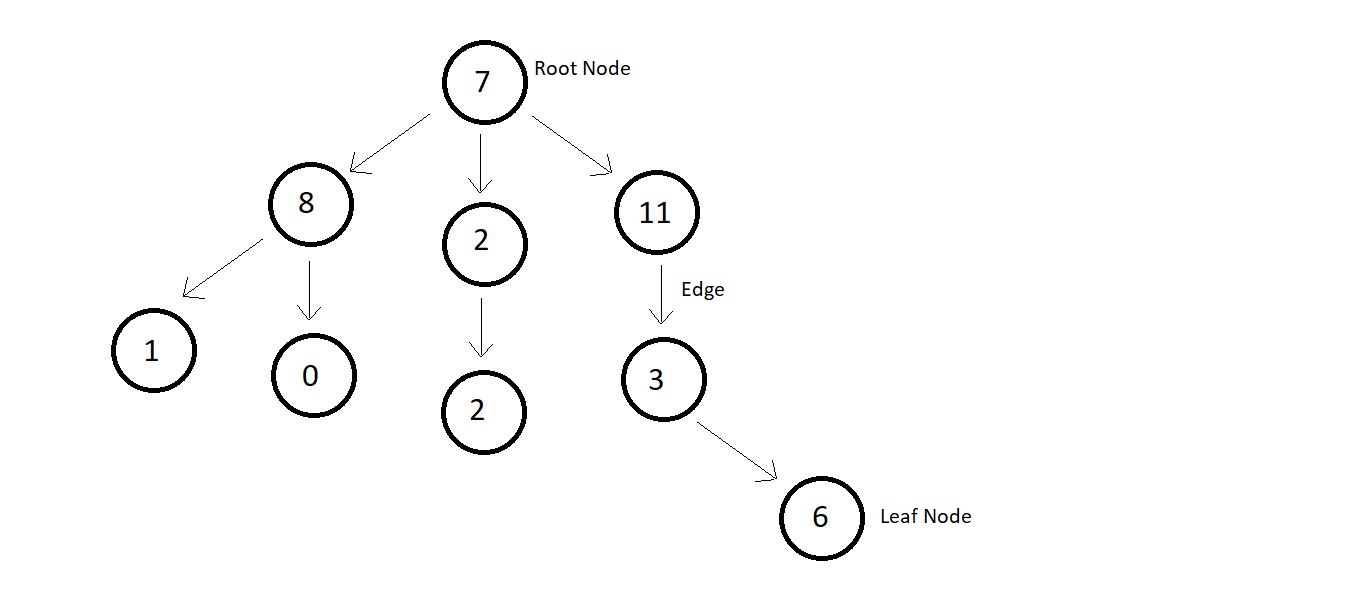
- A tree is made up of nodes and edges.
- The topmost node is called the Any node which points to another node, is the parent of that node and the node which the parent is pointing at is the child of that parent node. And nodes having the same parents are called siblings of each other.
- Nodes having zero children are the leaf nodes or the external nodes, and nodes having at least one child are the internal nodes.
- Ancestors of a node are the nodes accessible by traversing upwards along the edges. They are either the parents or the parents of the parents.
- Descendants of a node are the nodes accessible by traversing downwards along the edges. They are either the children or the children of the children.
- Height of a node is the number of edges in between the deepest leaf and that node. And depth of a node is the number of edges between the root and that node.
- The degree of a node in a tree is the number of children of a node.
- The degree of a tree is the highest degree of a node among all the nodes present in the tree.
Binary Tree
- A binary tree is a special type of tree where each node has a degree equal to or less than two which means each node should have at most two children.
Types of Binary Tree
- Full or Strict Binary Tree : have a degree of 2 or less than 2. But a strict binary tree is a binary tree having all of its nodes with a degree of 2 or 0. That is each of its nodes either have 2 children or is a leaf node.
- Perfect Binary Tree : A perfect binary tree has all its internal nodes with degree strictly 2 and has all its leaf nodes on the same level. (difference : 2 or 0 but here its only 2).
- Complete Binary Tree : A complete binary tree has all its levels completely filled except possibly the last level. And if the last level is not completely filled then the last level’s keys must be all left-aligned.
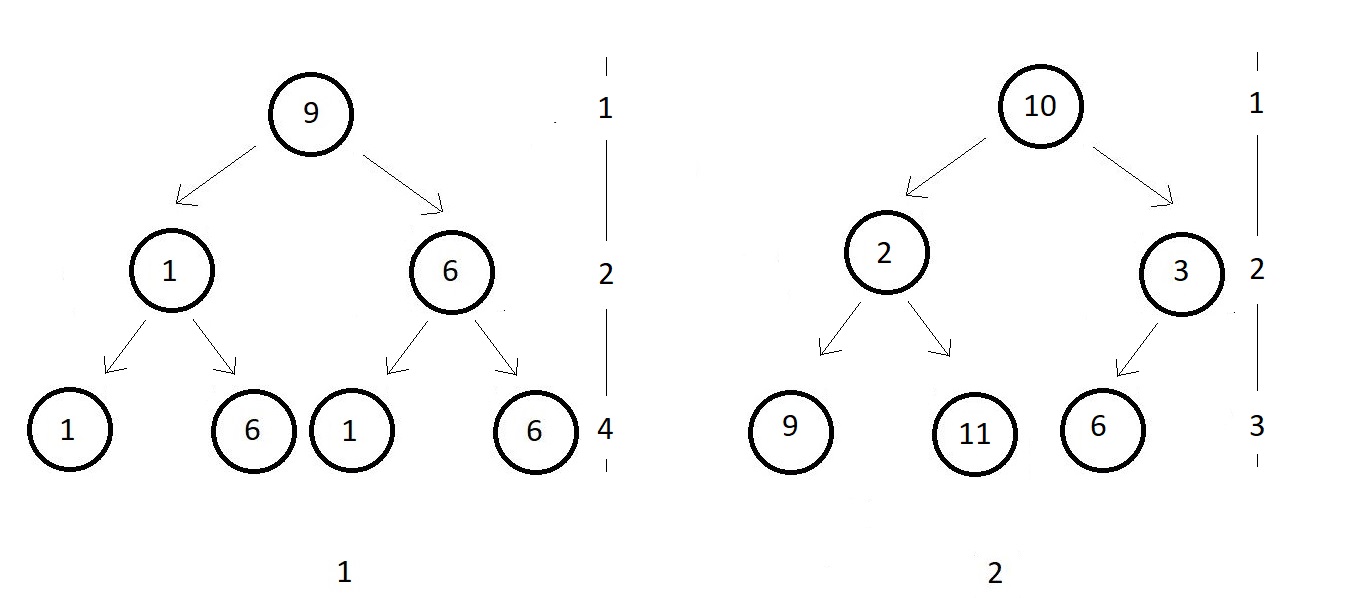
- As indicated in figure 1(down), all levels are completely filled, so nothing further needs to be done. It is a complete binary tree. In figure 2, all nodes are completely filled except the last level which has just 3 keys. It is nonetheless a complete binary tree because all keys are left-aligned.




